Catamorphism

F-algebras

Schoolofhaskell

type Algebra f a = f a -> a

Two really essential aspects of an algebra:

1. The ability to form expressions and
2. The ability to evaluate these expressions

Express a recursive data type as a non-recursive data type and a fixpoint operator.

newtype Fix f = Fx (f (Fix f))
-- often called Mu

data Tree' a t = Leaf a | Tree' [t]
type Tree a = Fix (Tree' a)

let x = Fx (Leaf 4) :: Tree Int

The type Fix F' is inhabited when there is one constructor of F' that doesn’t depend on t. (Here F' = Tree' a.)

Fx is a function f (Fix f) -> Fix f.

Abstract away recursion: we need a evaluation strategy alg :: f a -> a for each top-level construct and a way eval to evaluate its children. a is the carrier type of the algebra.

An F-algebra consists of:

1. an endofunctor F in a category C (e.g. of types),
2. an object A in that category (e.g. a type), and
3. a morphism from F(A) to A.

alg :: Algebra Tree' String -- Tree' String String -> String
alg (Leaf i) = i
alg (Tree i j) = printf "(%s,%s)" i j

This is a function F' a -> a where a = String, F' = Tree' String. We want a function F -> a. (F = Tree a) (In the image, f is F' and Fix f is F.

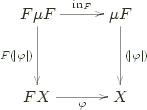
A note on Fx: It’s type is F' (Fix F') -> Fix F' = Algebra F' (Fix F'). (Note Fix F' = F.) It’s a non-lossy evaluator. It is “at least as powerful as all other algebras based on the same functor. That’s why it’s called the initial algebra.” There exists a unique homomorphism from it to any other algebra based on the same functor.

Catamorphisms (bananas)

Wiki

Generalization of fold.

Given alg, this function g is the catamorphism.

cata :: Functor f => (f a -> a) -> Fix f -> a
cata alg = alg . fmap (cata alg) . unFix

So

alg :: Algebra Tree' String -- Tree' String String -> String
alg (Leaf i) = i
alg (Tree i j) = printf "(%s,%s)" i j

print :: Tree String -> String
print = cata alg

Compare this to the usual way we’d write such a function (here Tree is defined without fixpoints)

print :: Tree String -> String
print = \case
	Leaf i -> i
	Tree i j -> printf "(%s,%s)" (print i) (print j)

Note: “Actually, even in Haskell recursion is not completely first class because the compiler does a terrible job of optimizing recursive code. This is why F-algebras and F-coalgebras are pervasive in high-performance Haskell libraries like vector, because they transform recursive code to non-recursive code, and the compiler does an amazing job of optimizing non-recursive code.”