Proofs and stories as obstacle avoidance

Back to Math communication

Proofs as obstacle avoidance

When you look at a proof written without motivation, it may look like a very windy path:

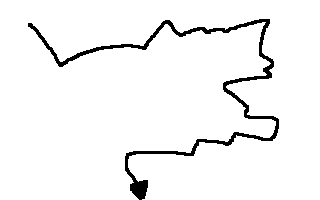
How would someone think to come up with such a complex proof? The answer is nicely encapsulated by the Simon’s ant metaphor.

“An ant, viewed as a behaving system, is quite simple. The apparent complexity of its behavior over time is largely a reflection of the complexity of the environment in which it finds itself”.

When you look at the obstacles to the proof, the path becomes a lot more motivated:

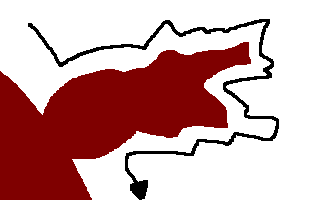
Thus, in teaching math it makes more sense to give proofs as successive approximations: first we’re going to try to the most direct path,

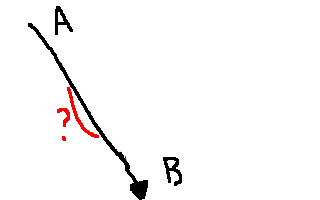
we’re going to see it doesn’t work

and then we’re going to successively refine our approach until we connect up our givens (A) and our desired (B).

(If you’re reading a math proof that’s given as in the first figure, then a good way to understand it is to try working on the problem yourself until you can see the shape of the obstacle, i.e., resupply the obstacle.)

Why should proofs be written “backwards”?

During an early stage in learning math, we learn that “you solve a problem backwards but you write it forwards.” This is very well for writing up homework problems, where the goal is to create a watertight argument. However, if you want to communicate a proof in a way such that other people will remember it and be able to re-apply the methods, then you should show a proof as obstacle avoidance.

Some more reasons:

• This refocuses math learning on the methods and the process, rather than the results. The methods are ultimately what transfers into tackling new problems.
• It is much easier to remember a proof if you can make the correspondence between the elements of the proof and the obstacles in the problem – which elements were introduced to combat which obstacles? You may have an illusion of understanding if you just see the windy path: when you put the text away, you can’t remember the windy path because you don’t know the rock it was trying to avoid!
• It is much easier to extract a concise proof from a proof written as backwards, than to extract the motivation from a proof written forwards.

Stories as obstacle avoidance

The metaphor given by the picture occurs in a lot of different settings. For example, when writing a story, it would be no fun if the characters got from point A to point B immediately! Here the obstacles aren’t simply existent like in math; the writer throws in a bunch of them to make the story more interesting, more windy… People like challenges; there is satisfaction to a path that makes it from A to B but is windy in the middle.